Patrick Keane – New Forest Knowledge

A simple algorithm to calculate acreage from the number of square links

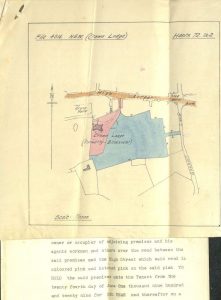
While the units of area based on the chain seem somewhat complex, there is an underlying simplicity behind them. The method below is an illustration of the algorithm, adapted from The Practical Surveyor by Samuel Wyld, published in 1725.

Let us say you have a parcel of land containing an area of 307960 square links.

a) Counting from the right, put a marker, perhaps a semi-colon, between the fifth and sixth character.

We obtain: 3;07960.

The acreage is the number to the left of the semi-colon.

Our parcel contains 3 acres and a bit more.

b) Multiply the number to the right of the semi-colon by 4 (the number of roods in an acre) to calculate the number of roods.

07960 x 4

We obtain: 31840.

Once again we place a semi-colon between the fifth and sixth character counting from the right.

There is no sixth character, so we insert a zero.

We obtain: 0;31840

The number of roods is the number to the left of the semi-colon. There are no roods.

Our parcel contains 3 acres, 0 roods and a bit more.

c) Multiply the number to the right of the semi-colon by 40 (the number of poles in a rood).

31840 x 40

We obtain: 1273600

Once again we place a semi-colon between the fifth and sixth character counting from the right.

12;73600

The number of poles is the number to the left of the semi-colon.

Our parcel contains 3 acres, 0 roods and 12 poles. And, for any obsessives, an aditional 73600 hundred thousandths of a pole, roughly the area of a double garage.

This algorithm simply requires us to be able to count the digits of a number from right to left and to be able to multiply by four.

It is a triumph of combining the decimal system with the traditional measurements of land.

An Accidental Discovery

When I was a young boy my mother brought me to Lyndhurst and showed me the house where she had lived as a young girl. All I could remember was that it was white, imposing and set in its own grounds. Fifty years later I moved to Brockenhurst and became interested in seeing if I could find the house.

My grandfather worked in coal logisitics, organising its delivery to strategic locations, mainly sea ports for the Royal Navy and merchant shipping. I knew that he never stayed long in any one place because his work took him all over Europe, and I knew also that he had never in fact owned a property.

I have been a volunteer in the Christopher Tower Reference Library in the New Forest Heritage Centre in Lyndhurst for six years now, and in quiet moments tried in vain to find any documentation which might point to where the family had lived.

Signature on lease

One of my recent jobs in the library has been preparing the digitised copies of the Forestry Commission records of leases (Lease Books) into bundles for entry into our Adlib database and for publication on the New Forest Knowledge website. I had just finished a bundle when I looked at the last page of a lease and there was my grandfather’s name and a signature.

Was it my grandfather? What was the probability that there were two people called Herbert Bamber leasing property in Lyndhurst at the same time?

There are strong similarities between the passport signature and that of the lease, but the capital Bs look quite different. Equally there is a long gap in time between the signatures. Page two of the lease gives Herbert’s address as No 1 Canute Road Southampton. Our library copy of Kelly’s Directory for Hampshire 1931 shows that 1 Canute Road was occupied by Clarke, Stephenson & Associated Co. Ltd, coal factors.

Now what is the probability that there were two people called Herbert Bamber, leasing property in Lyndhurst at the same time and both working in the coal industry? It begins to seem more like a certainty. We shall know for sure only in 2031 when we get access to the 1931 census.

The Bird's Nest So where is this property? It turns out to be Crown Lodge, now occupied by the New Forest Nondescripts Club, on Church Lane in Lyndhurst. It was originally called The Bird’s Nest for reasons which the photo make clear.

Further details about the building’s history can be found on the New Forest Knowledge website at:

https://nfknowledge.org/record/nfp-15/

Map of lease

The lease also shows that the land attached to the house comprises not just the basic property coloured red, but most of what is now the main Lyndhurst carpark coloured blue. Ironically, and somewhat irritatingly, three times while volunteering in the Library I have been fined for breaching parking regulations on land that was leased to my grandfather.

An Exhibition- Maps: the New Forest Unfolded

This exhibition reveals biographies of the New Forest and its people through maps selected from the collection of the Christopher Tower New Forest Reference Library.

These maps, of large and small scale, illuminate not only the landscape but the individuals and institutions that shaped the Forest as it is today.

Maps help us to understand our world: to navigate, to show ownership, to describe the function or value of spaces, to indicate their characteristics, to explain the past and to plan the future. Behind our maps lie the stories of their creators, characters who dedicated themselves to sharing their enthusiasms with an eager public.

Not only surveyors, but foresters, archaeologists, a pioneering motorist, and a dancing master with a broken leg have all contributed to the wealth of maps, plans and charts that display what was, what is and what might have been.

The exhibition covers seven broad themes:

Geology and Archaeology
The role of government in the 18th and 19th centuries
Place-names
Large scale mapping by the Ordnance Survey
Travel
What might have been
- Defoe and the Poor Palatines
Forestry Commission stock maps

Brockenhurst

‘grid_reference’:”,’shelf_mark’:’FF13-23-01′,’map_envelope’: ”,’map_category’: ‘Topographical’,’map_os_reference’: ”,’map_revision_date’: ”,’map_coverage’: ‘Brockenhurst’,’map_quoted_scale’: ‘1:2,500′,’map_fractional_scale’: ‘1:2,500′,’edition’: ‘Original on linen’,’comments’: ‘Showing proposed road alteration to allow a bypass around level crossing gates’,’map_annotated’: ”,’accession_number’: ”,’map_annotation_comment’: ”,’creator’: ‘Ordnance Survey’

Defoe and the Poor Palatines

In 1709 Britain experienced an influx of about 13,000 refugees, known as the poor Palatines, from Germany. They were largely protestant, fleeing from aggression by the catholic Louis XIV of France. Mainly these people hoped to continue their journey to America where other German refugees had found new homes in previous years.

The Whig party which controlled parliament at that time was of the opinion that an increase in population would help develop the economic wealth of the nation, while the Tory party was concerned that the number of these immigrants who were largely poor would lead to instability.

Portrait of Daniel Defoe, National Maritime Museum, London

Daniel Defoe, who was a leading radical thinker of the time, suggested that an area of the New Forest near Lyndhurst be set aside to create a model township for the refugees. Twenty honest and industrious men capable in husbandry would be identified and given 200 acres each. Known as farmers, these men would be given money to stock their farms and live rent and tax free for twenty years. Through the wealth they generated from their farming they would pay for the whole infrastructure of the town, including doctors, ministers of religion, carpenters, builders, a miller and other labourers: inn-keeping was expected to be a part-time occupation. In total Defoe expected that this scheme would support some six or seven hundred people. After twenty years when the town was established the residents would start to pay taxes.

Ultimately Defoe expected there to be about 20 such schemes built across the country.

The form of the several farms would be laid out thus.

Defoe’s sketch map shows the layout of the township, with the central crossroad housing the necessary infrastructure for the establishment of a flourishing community. He expected that common land would be available outside the perimeter to allow the tradespeople to keep a few cattle or sheep to help eke out their existence. The twenty farms are marked out, although the farm buildings are probably not to scale.

Nowadays few of us have an easy understanding of what 200 acres means. Far less do we understand the concept of 40,000 acres, not to mention the extent of land required for the Town Hall, church, labourers’ cottages and other pieces of infrastructure.

The map shows the extent of land that Defoe’s township would have covered if it were planted half way between Lyndhurst and Brockenhurst.

Defoe made an assumption that the soil of the new Forest was of sufficient quality to make his scheme work. In fact the reason for the New Forest’s survival as a wilderness is that the ground is generally of little agricultural merit.

Defoe’s, 1962, A Tour through the whole Island of Great Britain Vol-1 can be read online:

Defoe, D. 1927. A Tour through England and Wales: Divided into Circuits or Journies, Volume 1. London: Dent. G.915

Related contributions:

Digitisation of the Drivers’ Map of the New Forest

Published 1789 by William Faden, Geographer to the King. Surveyed by Thomas Richardson, William King, and Abraham and William Driver.

Scale: three and a half inches to one mile

One of the oldest maps in the Christopher Tower Library collection is known as the Drivers’ map after two of its original four surveyors. It was published in 1789 by William Faden, Geographer to the King, in support of a parliamentary report into the New Forest. At that time the forest was in a desperate condition, pulled apart by powerful conflicting interests. The Lord Warden of the New Forest was appointed to preserve the Forest for the King’s sport but was mainly concerned with dispensing patronage to loyal cronies. The Surveyor General of Woods had responsibility for the development of timber, mainly for the navy, and the generation of revenue for the state. Almost in despair at the contradictions within the management of the Forest, the Report draws the conclusion that no person would manage their own property in such a manner.

Parliament was determined to resolve this problem and commissioned a large scale map to help clarify the exact state of the forest. As well as marking the timber enclosures in the Forest, encroachments on Crown property were shown in red, crown leases in purple and intermediate land holdings in yellow. Such is the attention to detail in this map that even a misplaced boundary stone is recorded. Such is the accuracy that it was used as a base map for most parliamentary reports into the Forest for the following 75 years. Several later copies are also available in the library, showing the rolling program of enclosing and dis-enclosing parcels of woodland over the years.

The Map

Click on a tile to view a larger image. In some browsers a low resolution image may appear. Clicking again on the image will give a clear view of that tile. Each tile corresponds with one of the original 18 linen panels from which the map is constructed.

For a modern audience it is interesting to see the detail of the development of villages such as Burley, Wood Green and East Boldre from their original encroachments. Landmarks such as Puttle’s Bridge and the Naked Man near Wilverly Enclosure are clearly visible. It is also interesting to note that the word Enclosure is spelled on the map in the orthodox way as it is in Johnson’s Dictionary rather than Inclosure as it is written locally.

The Cartouche, the decorative title in the top right corner of the map, offers a summary of the political vision for the Forest’s future, confirming its role to be a place for growing naval timber. Components of the image include:

a crown at the top centre of the image
two woodsmen with axes
the broad arrow on a log in the foreground designating government property
a warship under construction
a plough and a harrow, the tools for preparing the enclosures for timber growth.

The only reference to the Forest’s previous function as a royal sporting ground is on the mound between the woodsmen and the oak tree. It is an image of the memorial to King William Rufus who died a violent and mysterious death while hunting in the Forest.

East Boldre Village Hall

East Boldre Village Hall is a Charitable Incorporated Organisation Registration No 11645494

East Boldre Village Hall is situated on open heathland in the New Forest National Park within the picturesque village of East Boldre. The historic building was built in 1917/18 as part of the Royal Flying Corps training airfield during WW1. It was used as an Officers’ Mess for entertainment with a lovely stage. At the end of the war when the other buildings demolished, the Officers’ Mess was left to the Villagers as a way of thanking them for their part in the war effort.

The Management Team

The East Boldre Village Hall is not a local authority facility. The building is run and maintained under Licence from the Forestry Commission by a small, friendly team of dedicated volunteers. We would appreciate as much of your help as you are willing to give. If you would like to join our team or help out in any way, please contact Steve Antczak (Secretary) using our Contact Page.

Forestry Commission Lease Books

Forestry England, the present land manager of the New Forest Crown Lands, has a collection of leases, easements, sales, and other contractual matters dating back to 1813. These documents have been copied and bound together in large lease books by the successive managers of the Forest- The Commissioners of Woods and Forests up to 1851, The Commissioners of Woods, Forests and Land Revenues from 1851-1919, and by the Forestry Commission from 1919 onwards up to the 1950s . The books are kept at the Queen’s House in Lyndhurst, but they cover more than just the New Forest. Nearby forests such as Bere and Alice Holt are included as well as others further afield such as those of Dean, Delamere, and even the Island of Alderney.

These records cover a period when the Forest underwent huge changes reflecting developments in society and technology. The first records date from the Napoleonic war when the supply of naval timber was critical for the survival of the nation. Once ships came to be built of iron this role was eclipsed and the Forest came to be valued more for its picturesque qualities. In the First World War the supply of Forest timber rapidly gained importance for its use in physically supporting the trenches and the light railways that brought supplies to the Western Front.

Under the Ecademy project, within the Our Past, Our Future Landcape Partnership scheme, supported by the National Lottery Heritage Fund, these records have been digitised.

The Christopher Tower Reference Library at the New Forest Heritage Centre has been preparing these records for publication on the web, and the first tranche, covering the period from 1813 to 1920, is now available on the New Forest Knowledge site. As well as showing how land use changed and developed over the century, these records cast light on the lives of the individuals and families who lived, worked and took their leisure in the forests, providing a rich resource for the family or social historian.

Altogether the leases comprise more than 40,000 pages of largely legalistic prose, containing often lengthy, repetitive sentences. Like the Shipping Forecast, their rhythm and cadence provide a sort of poetry. Often the documents are supported by hand sketched plans of the area in question. Only the most recent books are typed: the majority from this period are beautifully handwritten. None, however, can be searched digitally. Fortunately each book was comprehensively indexed at the time of its creation. Furthermore many of the later transactions have been inscribed in four Atlases covering the New Forest, so that a visual scan can often identify where a transaction has taken place.

Stop Press! Casual study has revealed the fact that not only are transactions about property recorded, but also employment contracts… See Lease Book 11, page 339, which records the extension of Lawrence Cumberbatch’s role as Deputy Surveyor of the New Forest to that of Deputy Surveyor of a string of other forests in the County of Southampton.

Please click on the links below to view some supplementary materials or click on the button to download them.

Notes on using the Lease Book Indexes Download

Notes on the Lease Book Atlases Download

Table of Contents for Forestry Lease Book Atlases Download

Click here to browse the full list of Lease Books and accompanying Atlases.

Maps for the traveller

New Forest

‘grid_reference’:”,’shelf_mark’:’FF13-22-05′,’map_envelope’: ”,’map_category’: ‘Historical’,’map_os_reference’: ”,’map_revision_date’: ”,’map_coverage’: ‘New Forest’,’map_quoted_scale’: ‘3 1/2″ to 1 mile’,’map_fractional_scale’: ‘[1:18,102]’,’edition’: ‘Original’,’comments’: ‘H.1789 B (i) and B (ii) are stored together in the box marked ‘only to be taken out in exceptional circumstances”,’map_annotated’: ”,’accession_number’: ”,’map_annotation_comment’: ”,’creator’: ‘Richardson, Thomas; King, William & Driver, Abraham & William’